円周上に要素を等間隔に並べる方法【jQuery・CSS】

2023/02/172024/02/22

円周上に要素を等間隔に並べたい！4つならCSSだけで簡単に配置できそうですが、それよりも数が多くなると。。。
ちょっと難しいですよね。
1年弱の間に「7つの要素を等間隔に並べる」という案件が2つもあったので、やり方をまとめてみました。

そんな案件、1年間で2つもあるの？？

ほんとすごい確率・・・w　偶然すぎますよねw

コード

今回は要素の数が7つですが、もちろん7つじゃなくても大丈夫です！

html


<div class=".big-circle">
	<p class="small-circle">1</p>
	<p class="small-circle">2</p>
	<p class="small-circle">3</p>
	<p class="small-circle">4</p>
	<p class="small-circle">5</p>
	<p class="small-circle">6</p>
	<p class="small-circle">7</p>
</div>

css

.big-circle {
	width: 400px;
	aspect-ratio: 1;
	border-radius: 50%;
	border: dashed 1px #777;
	margin: 50px;
	position: relative;
}

.small-circle {
	width: 80px;
	height: 80px;
	border-radius: 50%;
	background: #777;
	font-size: 32px;
	font-weight: 700;
	color: #fff;
	line-height: 80px;
	text-align: center;
	position: absolute;
	-webkit-transform: translate(-50%, -50%);
	transform: translate(-50%, -50%);
}

jQuery

$(function () {
	var item_num = $(".small-circle").length;
	var deg = 360.0 / item_num;
	var radians = (deg * Math.PI) / 180.0;
	var radians90 = (90 * Math.PI) / 180.0;
	var circle_r = $(".big-circle").width() / 2;
	$(".small-circle").each(function (i, elem) {
		var x = Math.cos(radians * i - radians90) * circle_r + circle_r;
		var y = Math.sin(radians * i - radians90) * circle_r + circle_r;
		$(elem).css("left", x);
		$(elem).css("top", y);
	});
});

jQuery部分をちょこっと解説

やっていることは、小さい丸の要素をposition:absolute;でtopとleftを指定してならべているのですが、topとleftを大きな外周円の中心からの座標を計算して指定しています。

円の中心からの座標は、三角関数で計算しているのですね！sinとか、cosとかですね！

三角関数！？！？

（遠い記憶。。。）

そして三角関数で使う角度ですが、JavaScriptで角度を取り扱う時は、単位をラジアンにするのが一般的です。

ラジアン！？！？

（遠い記憶。。。）

STEP

360度を要素の数（変数：item_num）で割り、円周を要素の数で割った際の円周角を求める。

var item_num = $(".small-circle").length;
var deg = 360.0 / item_num;

STEP

円周角をラジアン単位に変換する。

var radians = (deg * Math.PI) / 180.0;

Math.PIプロパティを使ってラジアン単位に変換します。もうこれはこういうもんってことで。

ラジアン単位への変換はこちらを参考にさせていただきました。

STEP

円の中心からの各要素の位置（x座標、y座標）を三角関数で計算する。

var x = Math.cos(radians * i) * circle_r;
var y = Math.sin(radians * i) * circle_r;

三角関数については、こちらを参考にさせていただきました。

STEP

親要素からの各要素への位置を計算し、CSSに位置情報を追加する。

var x = Math.cos(radians * i) * circle_r + circle_r;
var y = Math.sin(radians * i) * circle_r + circle_r;
$(elem).css("left", x);
$(elem).css("top", y);

STEP3の三角関数の計算で出てくる値は、大きな円の中心からのｘ座標とｙ座標です。実際には、親要素を基準にtopとleftで場所を指定するので、親要素の左上端から大きな円の中心までの距離（x方向に大きな円の半径分、y方向に大きな円の半径分）を足す必要があります。よって、var x、var y の最後にcircle_r(=円の半径)を足します！

この状態で表示されるのが、以下のイメージです。

STEP

必要に応じて、スタート場所を調整するために角度を調整する。

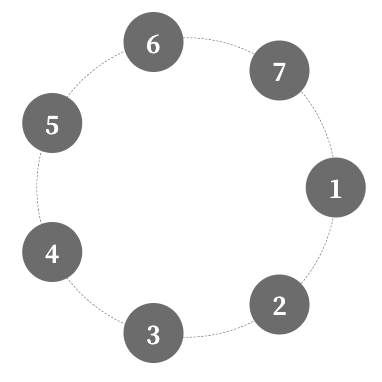
今回は７つの要素を並べますが、真上に１番目の要素が来てほしいので、９０度左にずらしたいと思います。

そこで、radians1という変数をラジアン角度で90度にし、座標を計算する際にその分を引くようにしました！

$(function () {
	var item_num = $(".small-circle").length;
	var deg = 360.0 / item_num;
	var radians = (deg * Math.PI) / 180.0;
	var radians90 = (90 * Math.PI) / 180.0;
	var circle_r = $(".big-circle").width() / 2;
	$(".small-circle").each(function (i, elem) {
		var x = Math.cos(radians * i - radians90) * circle_r + circle_r;
		var y = Math.sin(radians * i - radians90) * circle_r + circle_r;
		$(elem).css("left", x);
		$(elem).css("top", y);
	});
});

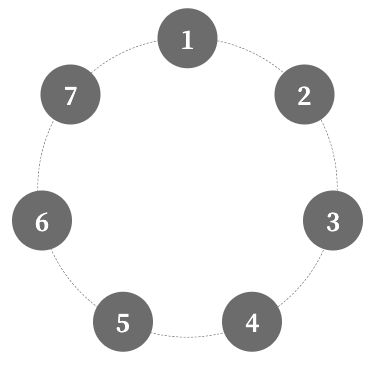
これで、真上から1番がスタートしましたね！